

If you would like to participate please contact us. Donations to the general fund to support those who cannot afford the cost of the test are welcome.
DNA STUDY


The concept of marker mutations confuses many at first glance. But it is actually quite simple, so we will attempt to explain the logic using the technique of 'expected values' - which is the long-run value taken over many independent repetitions.
Consider a lottery draw that has numbered balls from 1 to 300. You have bet on number 50. When the draw is held you would expect your number would be unlikely to come up. Your odds are 1/300, or 0.33%.
Let’s say that in the lottery, not one, but 44 balls are drawn. The odds of your number coming up are now 44/300 or roughly 1/7.
If you then do the same 44 draw every day for a week, you would expect that your number would come up once in that week, as you have 7 chances at 1/7 odds (7 * 1/7 =1 )
Now consider that the 44 balls are in fact the STR markers and that the 7 days are 7 generations. Using the same calculation, you would expect during the 7 generations that 1 mutation would occur on your own 44 markers. When comparing two people, each one could have 1 mutation, so the total expected mutations must be double that for one person, which is 2 mutations. So comparing two people over 7 generations with 44 markers tested, the expected number of mutations is 2. Easy now?
This logic can be distilled to a simple formula:
No of Markers tested x (No of generations x number of persons tested) x average mutation rate.
Sometimes the value of 'No of generations x number of persons tested' is rewritten as 'No of transmission events'. The transmission event value is simply the number of generations x the number of persons being compared. So for two 1st cousins, the most recent ancestor would be their grandfather. This would create 2 transmission events each, ie grandfather to father to son for each cousin. The total transmission events would be 4.
Back to our example , we can test the formula to predict the number of mutations in 2 people over 7 generations in a 44 marker test and using an average mutation rate of 0.33%
44 x (7x2) x 0.33/100 = 2.03. Or rounded, is 2 mutations.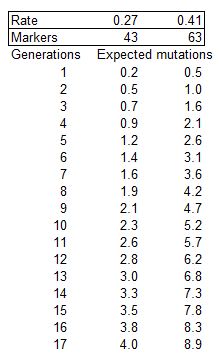
Or put it another way, the if you had 44 numbers in a 300 ball lottery, and there were two draws per day in a week, you would expect to win twice in that week.
We can use this formula to create a table of expected mutations in both the 44 and 67 marker tests. Note that the number of markers used in the calculations are actually 43 and 63, and not 44 and 67, as certain markers have several values so it is not certain where the mutation occurred, or indeed if it occurred, and it is standard practice to exclude these from calculations.
Using the table, for example, in a 63 marker comparison, using a mutation rate of 0.41%, the number of expected mutations where 11 generations exist between two parties tested, would be 6 (rounded as we cannot have 5.7 mutations). The expected result would therefore be 57/63 matching.
Caution on transmission events
Where there are more than two people being examined, the number of transmission events is not necessarily the number of generations multiplied by the number of people. There are two examples below where there are 10 transmission events.
The first has the same common ancestor and the transmission events are simply 2 x 5. However, if those being tested do not have a common ancestor then the calculation is not as straight forward.
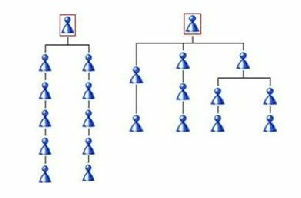
In the second example there are four people tested where the transmission events are not 12 (4 x 3) but are still 10. This is as the third and fourth people share a common ancestor one generation later than the first and second.
Therefore to calculate the number of transmission events for more than two people, where they do not all share the same common ancestor, the events must be counted manually to ensure that there is no double counting.